Bob si trova seduto su una panchina all’interno del parco, nutrendo i piccioni che si avvicinano. Improvvisamente, nota Alice che si avvicina mentre sta correndo al mattino.
“Come stai?” chiede a voce alta.
Alice risponde senza fiato: “Bene, ma ho appena sentito che un’armata proveniente dalla Galassia di Andromeda è diretta verso la Terra.”
Bob inizia a ridere e dice: “No, non può essere vero!”
Ma chi ha ragione? Secondo la teoria della relatività ristretta, potrebbero entrambi avere ragione, o entrambi essere sbagliati. Dipende dalla prospettiva.
Questo è noto come il paradosso di Andromeda, che rappresenta un esempio dell’argomento Rietdijk-Putnam descritto da Roger Penrose nel suo libro del 1989, “The Emperor’s New Mind“. Questo paradosso dimostra la perdita di simultaneità prevista dalla teoria della relatività ristretta.
Paradosso di Andromeda
Ecco come funziona.
L’accadere simultaneo o successivo di due eventi può variare a seconda del punto di osservazione. Nel caso in cui Alice si stia muovendo rispetto a Bob, dall’angolazione di Alice l’armata ha già iniziato la sua missione sfortunata, mentre dall’angolazione di Bob l’armata non è ancora partita.
La teoria della relatività ristretta si basa su due assiomi fondamentali:
- Tutti i punti di osservazione sono uguali.
- La velocità della luce è la stessa in ogni sistema di riferimento.
Da un punto di osservazione differente, Bob potrebbe risultare fermo mentre Alice si muove, mentre invece dall’angolazione di Alice, è Bob a risultare fermo e lei in movimento. Nessuno dei due punti di osservazione ha uno status privilegiato per descrivere gli eventi che accadono ad Andromeda.
Piuttosto che concentrarci sulla teoria, ci concentreremo direttamente sulla sua applicazione, dimostrando così le sue implicazioni.
Alice e Bob stanno esplorando la teoria della relatività ristretta
Un giorno, Alice e Bob decidono di fare una visita alla stazione ferroviaria. Alice è molto interessata a guidare la locomotiva chiamata “Light Speed” che ha la capacità di raggiungere velocità estremamente vicine a quella della luce. Bob, d’altro canto, è più cauto e preferisce aspettare sulla piattaforma.
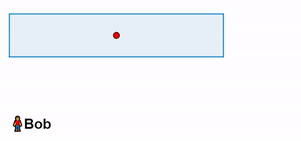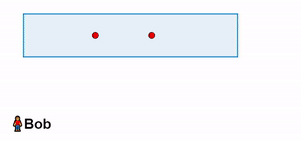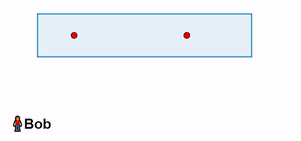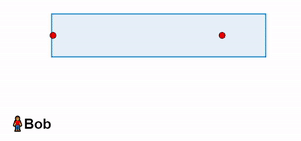
All’interno del vagone, ci sono due laser posizionati al centro. Mentre Alice passa accanto a Bob, i due laser emettono due brevi lampi di luce. Uno di essi viene proiettato verso la parte anteriore del vagone, mentre l’altro viene proiettato verso la parte posteriore.
Alice osserva i due impulsi di luce che colpiscono contemporaneamente le estremità del vagone.
Il treno ha due orologi posti agli estremi del vagone che registrano l’ora di arrivo degli impulsi, la quale risulta essere esattamente mezzogiorno. Tuttavia, Bob nota qualcosa di diverso: dalla sua prospettiva, il vagone si muove.
Nonostante la velocità degli impulsi luminosi sia uguale (Assioma 2), Bob osserva che la parte posteriore del vagone si muove verso il suo polso sinistro, mentre la parte anteriore si allontana dal polso destro. Di conseguenza, Bob registra che il polso sinistro arriva prima del polso destro.
In seguito, Bob e Alice confrontano le loro note. Bob nota che è strano che entrambi gli orologi indicano le 12:00. I due hanno raggiunto la loro destinazione in momenti diversi.
Alice guarda Bob con aria sbalordita.
Decidono quindi di guardare il video registrato con il telefono di Bob. L’orologio a sinistra riceve l’onda luminosa per primo e segna le 12:00, mentre l’orologio a destra riceve l’onda successiva e segna anch’esso le 12:00. Con grande sorpresa, scoprono che gli orologi non sono sincronizzati. L’orologio posteriore è in anticipo rispetto a quello anteriore.
Questa è un’effetto della relatività. Nel punto di vista di Alice, lei era ferma e gli orologi erano sincronizzati. Nel punto di vista di Bob, invece, l’orologio posteriore era in anticipo rispetto a quello anteriore. Chi ha ragione? Entrambi? Nessuno dei due? La simultaneità dipende dal punto di vista. Né Bob né Alice possono vantare un punto di vista privilegiato (Assioma 1).
Ora quantificheremo questo effetto.
Come calcolare la perdita di simultaneità
Immaginiamo di avere un vagone, di lunghezza L, che si sposta alla velocità v rispetto ad un osservatore esterno, Bob. In entrambi i sistemi di riferimento, la velocità della luce è costante e pari a c.
In quale posizione andrebbe collocata la fonte luminosa affinché i due estremi del vagone vengano illuminati simultaneamente nel sistema di riferimento di Bob?
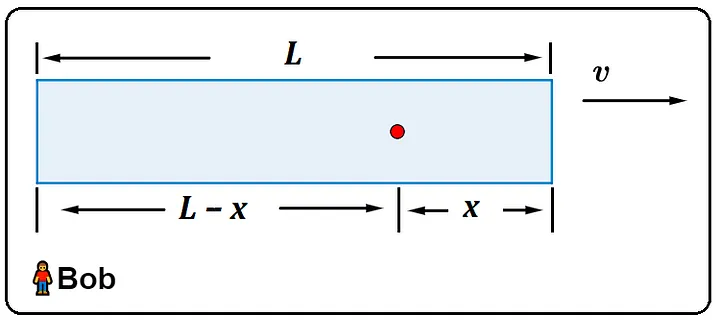
La lunghezza della distanza tra la fonte di luce e la parte anteriore del vagone è indicata con la variabile x, mentre la lunghezza della distanza tra la fonte di luce e la parte posteriore del vagone è indicata con la variabile Lx. Per Bob, il tempo impiegato da ciascun impulso luminoso è uguale.
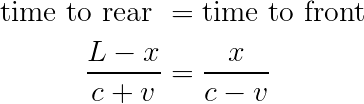
La velocità del vagone viene sommata o sottratta dalla velocità della luce, a seconda della direzione in cui l’impulso luminoso si sta muovendo.
Ora è possibile eseguire alcuni calcoli algebrici sull’espressione precedente.
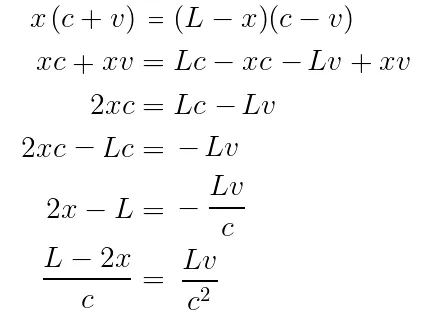
Cosa dobbiamo pensare dell’espressione finale? Nell’inquadratura di Alice, la parte anteriore del vagone viene colpito per primo dall’impulso. L’altro impulso, invece, ha percorso una distanza x verso la parte posteriore del vagone. Dovrà quindi percorrere un’altra distanza, pari a L-2x. Quindi, possiamo calcolare il ritardo del secondo impulso dividendo L-2x per la velocità della luce.
Per esempio, supponiamo che l’orologio anteriore segni le 12:00. L’orologio posteriore segna le 12:01, e Alice e Bob concordano su queste letture. Tuttavia, Bob registra gli impulsi che arrivano simultaneamente. L’orologio posteriore segna le 12:01 quando l’orologio anteriore segna le 12:00. Quindi, l’orologio posteriore è in anticipo.
L’espressione a destra ci dà le stesse informazioni, ma richiede solo di conoscere L e v per calcolare la differenza di tempo tra i due orologi. Poiché il risultato è positivo, significa che l’orologio posteriore è in anticipo.
Tornando all’incontro di Alice e Bob al parco.
Perché Alice osserva gli eventi prima di Bob.
Alice e Bob concordano raramente sulla simultaneità. Nella loro vita quotidiana, le distanze e le velocità coinvolte sono così piccole rispetto a c² che non ci sono problemi. Tuttavia, la Galassia di Andromeda è situata a una distanza di 2,5 milioni di anni luce.
Supponiamo che Alice si avvicini a Bob a una velocità di 5 m/s. (La Galassia di Andromeda si sta avvicinando alla Terra a una velocità molto più elevata. Tuttavia, ci interessa solo la differenza di tempo tra i fotogrammi di Bob e Alice.) Possiamo calcolare tale differenza di tempo:
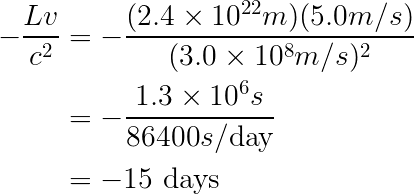
Considerazioni da fare
- È possibile intrattenere una discussione significativa riguardo a ciò che sta accadendo in questo momento in una galassia situata molto, molto lontano?
- Quali conseguenze avrebbe se Alice girasse e corresse nella direzione opposta?
- Bob potrebbe utilizzare le informazioni di Alice per scommettere sulle corse di cavalli di Andromeda?
- Quali sarebbero le implicazioni se Alice e Bob fossero in grado di inviare e ricevere un segnale più veloce della luce proveniente da Andromeda?
A cura di Ufoalieni.it
[…] In conclusione, l’illusione della scala di Penrose è un esempio affascinante di come il cervello elabora le informazioni visive. La figura sembra rappresentare un oggetto fisicamente impossibile, ma in realtà è il risultato della nostra percezione visiva. […]